Kako izračunati prosječnu brzinu: 12 koraka (sa slikama)

2024 Autor: Jason Gerald | [email protected]. Zadnja izmjena: 2024-02-01 14:12

Sve što vam je potrebno za izračunavanje prosječne brzine je ukupni pomak. ili promjena položaja i ukupno vrijeme. Upamtite da brzina također izračunava smjer i brzinu objekta, pa u svoj odgovor uključite smjer, poput "sjever", "sprijeda" ili "lijevo". Ako vaš problem izračunavanja brzine uključuje i stalno ubrzavanje, možete naučiti brz način da još lakše pronađete odgovor.

Korak

Metoda 1 od 2: Izračunavanje prosječne brzine pomaka i vremena

Korak 1. Zapamtite da brzina uključuje i brzinu i smjer objekta

Brzina opisuje brzinu kojom se mijenja položaj objekta. To nema veze samo s brzinom kretanja objekta, već i s njegovim smjerom. "100 metara u sekundi prema jugu" različita je vrijednost brzine od "100 metara u sekundi prema istoku".

• Veličine koje imaju smjer nazivaju se vektorske veličine '. Ova veličina se može razlikovati od veličine bez smjera koja se naziva skalarna veličina ispisivanjem strelice iznad varijable. Na primjer, oznaka v predstavlja brzinu, dok oznaka v ^→ predstavlja brzinu ili brzinu + smjer. V oznaka korištena u ovom članku predstavlja brzinu.
• U naučnim problemima trebali biste koristiti metre ili druge metričke jedinice za izražavanje udaljenosti, dok u svakodnevne svrhe možete koristiti bilo koju jedinicu koja vam se sviđa.

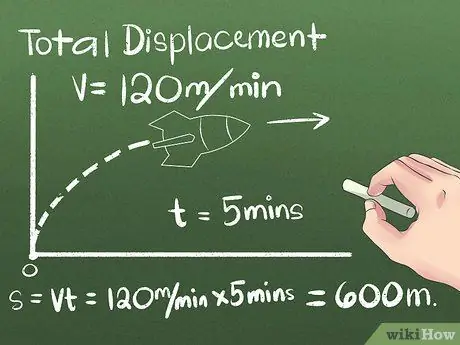
Korak 2. Pronađite ukupnu vrijednost pomaka

Pomak je promjena položaja objekta ili udaljenosti i smjera između njegove početne i završne točke. Smjer kojim se objekt kreće prije nego što dosegne svoj konačni položaj može se zanemariti, jer se uzima u obzir samo udaljenost između početne i krajnje točke. U prvom primjeru koristit ćemo objekt koji se kreće konstantnom brzinom u jednom smjeru:

• Recimo da se raketa kreće 5 minuta prema sjeveru konstantnom brzinom od 120 metara u minuti. Za izračun konačnog položaja upotrijebite formulu s = vt ili pomoću praktičnog razmišljanja izračunajte udaljenost koju je raketa prešla nakon toga (5 minuta) (120 metara/minuti) = 600 metara sjeverno od početne tačke.
• Za probleme koji uključuju konstantno ubrzanje, možete ih riješiti s s = vt + at²ili upotrijebite kratku metodu opisanu u drugom odjeljku da pronađete odgovor.

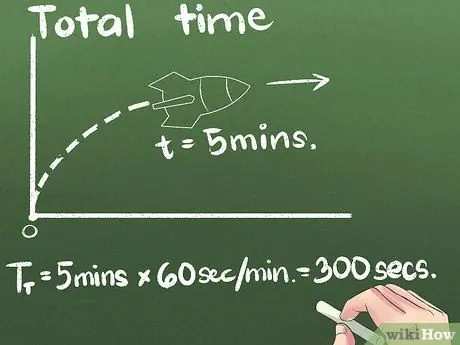
Korak 3. Pronađite ukupno vrijeme provedeno

U našem primjeru, raketa se kreće 5 minuta naprijed. Prosječnu brzinu možete izraziti u bilo kojoj jedinici vremena, ali druga je jedinica međunarodnog naučnog standarda. U ovom primjeru promijenit ćemo jedinice sekundi: (5 minuta) x (60 sekundi/minuti) = 300 sekundi.

Čak i u naučnim problemima, ako pitanje koristi sat ili veću jedinicu vremena, bit će lakše prvo izračunati brzinu, a zatim konačni odgovor pretvoriti u metre/sekundu

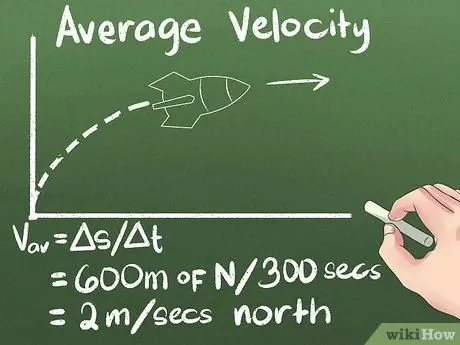
Korak 4. Izračunajte prosječnu brzinu kao pomak tokom vremena

Ako znate koliko se objekt kreće i koliko mu je potrebno da stigne tamo, znat ćete koliko se brzo kreće. Dakle, za primjer koji koristimo, prosječna brzina rakete je (600 metara sjeverno) / (300 sekundi) = 2 metra/sekundi sjeverno.

• Ne zaboravite uključiti smjer (kao što je "sprijeda" ili "sjever").
• U formuli v_av = s/Δt. Simbol delta znači "promjena", pa s/Δt znači "promjena položaja u određenom vremenskom periodu".
• Prosječna brzina se može napisati kao v_av, ili kao v sa vodoravnom linijom iznad.

Korak 5. Riješite složenije probleme

Nemojte se zbuniti ako objekt promijeni smjer ili brzinu. Prosječna brzina se i dalje "samo" računa iz ukupnog pomaka i ukupnog vremena. Ono što se događa između početne i završne točke možete zanemariti. Slijedi nekoliko primjera objekta koji putuje s istim pomakom i ukupnim vremenom, a time i istom prosječnom brzinom:

• Anna hoda 2 metra na zapad brzinom od 1 metra u sekundi, zatim iznenada ubrzava do 3 metra u sekundi i nastavlja hodati prema zapadu 2 sekunde. Ukupno pomicanje je (1 m/s zapadno) (2 sek) + (3 m/s zapadno) (2 sek) = 8 metara zapadno. Ukupno vrijeme je 2 sekunde + 2 sekunde = 4 sekunde. Dakle, prosječna brzina je 8 metara zapadno/ 4 sekunde = 2 metra/sekundi zapadno.

• Bart hoda 3 minute prema zapadu brzinom od 5 metara/sek, zatim se okreće i hoda prema istoku brzinom od 7 metara/sekundi 1 sekundu. Kretanje prema istoku možemo smatrati "negativnim kretanjem prema zapadu" pa je ukupni pomak = (5 metara/sek prema zapadu) (3 sek) + (-7 m/s zapadno) (1 sek) = 8 metara. Ukupno vrijeme = 4 sekunde. Prosječna brzina = 8 metara zapadno / 4 sekunde = 2 metra/sekundi zapadno.

• Charlotte je hodala sjeverno 1 metar, a zatim je hodala zapadno 8 metara, pa južno 1 metar. Za kompletno putovanje potrebno je 4 sekunde. Nacrtajte dijagram na komadu papira i vidjet ćete da je krajnja tačka 8 metara zapadno od početne tačke, pa je ova vrijednost pomak. Ukupno vrijeme potrebno je 4 sekunde, pa je prosječna brzina 8 metara zapadno / 4 sekunde = 2 metra/sekundi zapadno.

  Metoda 2 od 2: Izračunavanje prosječne brzine fiksnog ubrzanja

  

  Korak 1. Razmotrite početnu brzinu i konstantno ubrzanje

  Recimo da je naš problem "Bicikl se kreće udesno brzinom od 5 m/s, uz konstantno ubrzanje od 2 m/s². Ako se ovaj bicikl kreće 5 sekundi, kolika mu je prosječna brzina?"

  Ako je jedinica "metar/sekunda²"da vas zbuni, napišite to kao" metara/sekundi/sekundi "ili" metara u sekundi u sekundi. "Ubrzanje od 2 metra/sekundi/sekundi znači da se brzina svake sekunde povećava za 2 metra u sekundi.

  

  Korak 2. Koristite ubrzanje da biste pronašli konačnu brzinu

  Ubrzanje, označeno oznakom a, je stopa promjene brzine (ili brzine). Brzina se konstantno povećava. Možete nacrtati tablicu pomoću ubrzanja kako biste pronašli brzinu u različito vrijeme tijekom biciklističkog putovanja. Moramo stvoriti ovu tablicu kako bismo pronašli krajnju točku problema (pri t = 5 sekundi), ali stvorit ćemo dužu tablicu kako biste lakše shvatili ovaj koncept:

  • Na početnoj točki (vrijeme t = 0 sekundi), bicikl se kreće brzinom od 5 metara/s.
  • Nakon 1 sekunde (t = 1), bicikl se kreće brzinom od 5 metara/sekundi + pri = 5 metara/sekundi + (2 metra/sekundi)²) (1 sekunda) = 7 metara/sekundu.
  • Pri t = 2, bicikl se kreće udesno brzinom 5+ (2) (2) = 9 metara/sek.
  • Pri t = 3, bicikl se kreće udesno brzinom 5+ (2) (3) = 11 metara/sek.
  • Pri t = 4, bicikl se kreće udesno brzinom 5+ (2) (4) = 13 metara/sek.
  • Pri t = 5, bicikl se kreće udesno brzinom 5+ (2) (5) = 15 metara u sekundi.

  

  Korak 3. Pomoću ove formule pronađite prosječnu brzinu

  Ako i "samo" ako je ubrzanje konstantno, prosječna brzina bit će jednaka prosječnoj vrijednosti zbira konačnih i početnih brzina. (v_f +v_i)/2. Za naš gornji primjer problema, početna brzina bicikla je v_i 5 metara u sekundi. Nakon što izračunamo, konačna brzina je v_f 15 metara u sekundi. Sabiranjem ove dvije vrijednosti dobivamo (15 metara/sekundi + 5 metara/sekundi)/2 = (20 metara/sekundi)/2 = 10 metara/drugi desni smjer.

  • Ne zaboravite uključiti smjer, u ovom slučaju "desno".
  • Ovaj izraz se može napisati kao v₀ (brzina u trenutku 0, ili početna brzina) i v (konačna brzina).

  

  Korak 4. Intuitivno shvatite formulu prosječne brzine

  Da bismo pronašli prosječnu brzinu, možemo upotrijebiti brzinu u bilo kojoj točki i pronaći prosjek za sve njih. (Ovo je definicija prosjeka.) Budući da je za to potreban račun ili beskonačno vrijeme, shvatite ovu formulu intuitivnije. Umjesto da uzimate svaki put, izračunajte prosječnu brzinu dviju vremenskih točaka i pogledajte rezultate. Jedan trenutak je blizu početka vožnje, gdje se bicikl polako kreće, a drugi trenutak blizu krajnje točke gdje bicikl ide brzo.

  

  Korak 5. Testirajte intuitivnu teoriju

  Pomoću gornje tablice odredite brzinu u različitim vremenskim trenucima. Neki parovi koji zadovoljavaju naše kriterije su (t = 0, t = 5), (t = 1, t = 4) ili (t = 2, t = 3). Ovu formulu možete testirati i s t vrijednostima osim cijelih, ako želite.

  Koji god par tačaka izaberete, prosječna brzina u to vrijeme će uvijek biti ista. Na primjer, ((5+15)/2), ((7+13)/2) ili ((9+11)/2) su sve jednake 10 metara/s desno

  

  Korak 6. Dovršite intuitivno objašnjenje

  Ako koristimo ovu metodu sa spiskom svakog puta, nastavit ćemo s izračunavanjem prosjeka prve polovine putovanja i druge polovine putovanja. Vrijeme potrebno za pokrivanje svake polovine je isto, pa se brzina ne gubi kada završimo odbrojavanje.

  • Budući da će oba para dati isti rezultat, prosjek ovih brzina također će biti vrijedan. U našem primjeru, brzina cjeline je "10 metara/sek nadesno" i dalje će biti 10 metara/sek nadesno.
  • Ovu vrijednost možemo pronaći izračunavanjem prosjeka bilo kojeg para, na primjer početne i krajnje brzine. U našem primjeru, ove se brzine postižu pri t = 0 i t = 5, a mogu se izračunati pomoću gornje formule: (5+15)/2 = 10 metara/s desno.

  

  Korak 7. Shvatite ovu formulu matematički

  Ako vam je ugodnije s dokazima zapisanim kao formule, možete započeti s formulom za izračunavanje prijeđene udaljenosti pod pretpostavkom konstantnog ubrzanja i odatle izvesti formulu:

  • s = v_it + at². (Tehnički s i t, ili promjena položaja i promjena u vremenu, ali i vas bi razumjeli da ste napisali s i t.)
  • Prosječna brzina v_av definirano kao s/t, pa formulu unesite u obliku s/t.
  • v_av = s/t = v_i + at
  • Ubrzanje x vrijeme jednako je promjeni ukupne brzine, ili v_f - v_i. Tako možemo zamijeniti "at" u formuli i dobiti:
  • v_av = v_i + (v_f - v_i).
  • Pojednostavite: v_av = v_i + v_f - v_i = v_i + v_f = (v_f +v_i)/2.

  Savjeti

  • Brzina se razlikuje od brzine jer je brzina vektorska veličina dok je brzina skalarna veličina. Vektorske veličine uključuju i smjer i veličinu, dok skalarne veličine uključuju samo veličinu.
  • Ako se objekt kreće u jednoj dimenziji, kao što je lijevo-desno, možete koristiti pozitivan broj za predstavljanje jednog smjera (kao što je desno) i negativan broj za predstavljanje drugog smjera (lijevo). Napišite ovu notaciju na vrh stranice tako da bude jasno ljudima koji čitaju vaš rad.