- Autor Jason Gerald [email protected].
- Public 2024-02-01 14:12.
- Zadnja izmjena 2025-01-23 12:08.
Pomak u fizici označava promjenu položaja objekta. Kada izračunate pomak, računate koliko je udaljen objekt na osnovu njegovih početnih i konačnih lokacija. Formula koju koristite za izračunavanje pomaka ovisi o varijabli datoj problemu. Slijedite ove korake za izračun pomaka.
Korak
Dio 1 od 5: Izračunavanje rezultirajućeg pomaka

Korak 1. Koristite rezultirajuću formulu pomaka ako se jedinica udaljenosti koristi za označavanje vaše početne i završne lokacije
Iako se udaljenost razlikuje od pomaka, rezultirajući problem pomaka traži koliko je kilometara ili metara objekt prešao. Ovu mjernu jedinicu ćete koristiti za izračunavanje pomaka i udaljenosti lokacije objekta od početne tačke.
- Rezultirajuća formula pomaka se zapisuje kao: S = x²+y². S je pomak. X je prvi smjer kretanja objekta, a Y drugi smjer kretanja objekta. Ako se vaš objekt pomiče samo u jednom smjeru, tada je Y = 0.
- Objekt se može kretati samo u najviše dva smjera jer se kretanje po osi sjever/jug ili istok/zapad smatra neutralnim kretanjem.

Korak 2. Spojite točke po redoslijedu kretanja i označite ih od A-Z
Pomoću ravnala nacrtajte ravnu liniju od tačke do tačke.
- Takođe ne zaboravite da povežete početnu tačku sa krajnjom tačkom ravnom linijom. Ovo pomjeranje ćemo izračunati.
- Na primjer, ako se objekt pomiče istočno 300 m i sjeverno 400 m, formirat će pravi trokut. AB će biti prvi krak trokuta, a BC će biti drugi krak. AC će biti hipotenuza trokuta, a njegova veličina je pomak objekta. U ovom primjeru dva su smjera istočni i sjeverni.

Korak 3. Unesite vrijednosti za x² i y²
Sada kada znate dva smjera kretanja vašeg objekta, unesite vrijednosti u odgovarajuće varijable.
Na primjer, x = 300 i y = 400. Formula bi trebala izgledati ovako: S = 300² + 400²
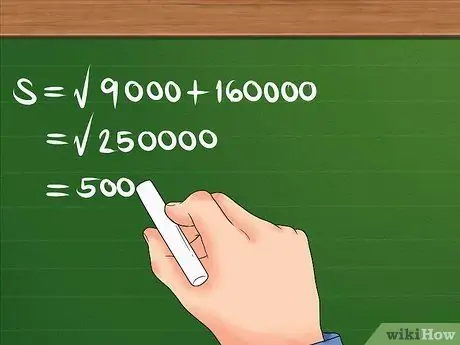
Korak 4. Izračunajte formulu prema redoslijedu operacija
Prvo kvadrirajte 300 i 400, zatim ih zbrojite i pronađite kvadratni korijen zbroja.
Na primjer: S = 90000 + 160000. S = 250000. S = 500. Sada znate da je pomak 500 m
Dio 2 od 5: Kad su brzina i vrijeme poznati

Korak 1. Koristite ovu formulu kada vam problem kaže brzinu objekta i vrijeme potrebno
Neki matematički problemi neće vam reći koliko daleko ili koliko se brzo objekt kreće. Pomoću ove veličine vremena i brzine možete izračunati pomak.
-
U ovom slučaju formula postaje: S = 1/2 (u + v) t.
U = početna brzina objekta ili brzina kojom se objekt počinje kretati u određenom smjeru. V = konačna brzina objekta ili koliko se brzo objekt kreće prema svojoj konačnoj lokaciji. T = vrijeme potrebno objektu da dođe do svoje konačne lokacije.
- Primjer: Automobil ide niz cestu 45 sekundi (potrebno vrijeme). Automobil skreće na zapad brzinom 20 m/s (početna brzina), a na kraju ceste njegova brzina je 23 m/s (konačna brzina). Izračunajte pomak na temelju ovih faktora.

Korak 2. Unesite potrebnu brzinu i vrijeme u odgovarajuće varijable
Sada kada znate koliko se automobil kreće, koliko se brzo kreće na početku i na kraju, možete pronaći udaljenost od početne do konačne lokacije.
Vaša formula bi trebala izgledati ovako: S = 1/2 (20 + 23) 45

Korak 3. Izračunajte formulu nakon što postavite vrijednosti na pravo mjesto
Ne zaboravite slijediti redoslijed operacija, inače će pomaci rezultirati vrlo različitim vrijednostima.
- Za ovu formulu nije važno ako ste slučajno promijenili početnu i završnu brzinu. Budući da ćete ove brojeve prvo zbrajati, nije važno gdje se nalaze u zagradama. Međutim, za druge formule, zamjena početne i krajnje brzine rezultirat će različitim vrijednostima pomaka.
- Vaša formula bi trebala izgledati ovako: S = 1/2 (43) 45. Prvo podijelite 43 na 2, što će rezultirati 21, 5. Zatim pomnožite 21, 5 sa 45, tako da je rezultat 967,5 metara. 967, 5 je veličina vašeg pomaka ili koliko se vaš automobil pomaknuo od početne tačke.
Dio 3 od 5: Kada su poznata početna brzina, ubrzanje i vrijeme
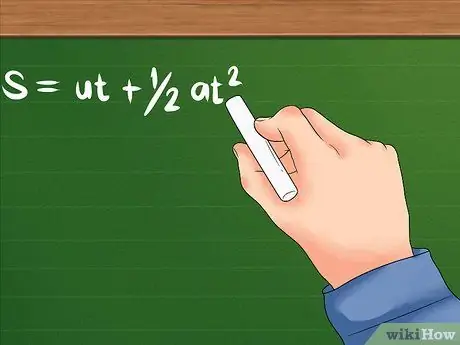
Korak 1. Upotrijebite izmijenjenu formulu ako je ubrzanje poznato uz početnu brzinu i vrijeme
Neka pitanja će vam samo reći koliko se brzo objekt kreće na početku, koliko brzo objekt počinje ubrzavati i koliko se objekt kreće. Trebat će vam sljedeća formula.
- Formula za ovaj problem je: S = ut + 1/2at². U i dalje označava početnu brzinu; a je ubrzanje objekta ili koliko se brzo njegova brzina počinje mijenjati. T može značiti vrijeme potrebno ili određeno vrijeme potrebno za ubrzanje objekta. Obje će koristiti vremenske jedinice kao što su sekunde, sati i druge.
- Pretpostavimo da automobil koji se kreće brzinom 25 m/s (početna brzina) počne ubrzavati brzinom od 3 m/s2 (ubrzanje) 4 sekunde (vrijeme). Koliki je pomak automobila nakon 4 sekunde?

Korak 2. Unesite vrijednosti u formulu
Za razliku od prethodne formule, ovdje je prikazana samo početna brzina, stoga svakako unesite točne podatke.
Na osnovu gornjih uzoraka, vaša formula bi izgledala ovako: S = 25 (4) + 1/2 (3) 4². Pomaže dodavanje zagrada oko veličine ubrzanja i vremena kako biste lakše odvojili brojeve
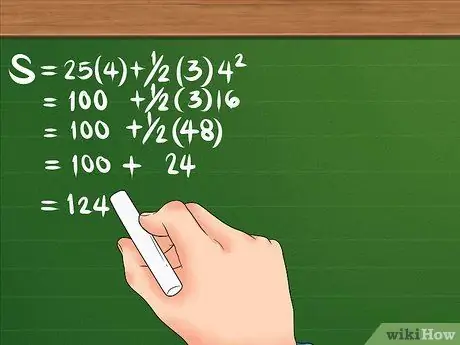
Korak 3. Izračunajte pomak radeći to ispravnim redoslijedom operacija
Brz način da vam zapamtite slijed operacija je magareći most Kur ir Kua ci Kadang Ba wa Juragan Turtles. Ovo predstavlja ispravan redoslijed: zagrade, kvadrate, množenje, dijeljenje, sabiranje i oduzimanje.
Pogledajmo formulu ponovo: S = 25 (4) + 1/2 (3) 4². Prvo, kvadrat 4, rezultat je 16. Zatim, pomnožite 16 sa 3, čineći 48; zatim također pomnožite 25 sa 4, kako biste dobili 100. Podijelite 48 sa 2, kako biste dobili 24. Vaša jednadžba bi trebala izgledati ovako: S = 100 + 24. Kada zbrojite to dvoje, pomak je 124 metra
Dio 4 od 5: Izračunavanje kutnog pomaka

Korak 1. Pronađite kutni pomak dok se objekt kreće po kružnoj putanji
Iako ćete i dalje računati pomak ravnom linijom, morat ćete pronaći razliku između početne i završne lokacije objekta dok se kreće po kružnoj putanji.
- Zamislite djevojku koja sjedi na vrtešci. Dok se okreće s vrtuljkom, kretat će se kružnom putanjom. Kutni pomak pokušava pronaći najkraću udaljenost između početne i krajnje lokacije kada se objekt ne kreće ravno.
- Formula za kutni pomak je: = S/r, gdje je S linearni pomak, r je polumjer, a kutni pomak. Linearni pomak je koliko se objekt kreće duž luka. Radijus je udaljenost objekta do središta kruga. Kutni pomak je vrijednost koju želimo pronaći.

Korak 2. Uključite linearni pomak i polumjer u jednadžbu
Upamtite da je radijus udaljenost od središta kruga; neki problemi će vam reći promjer kruga, koji se mora podijeliti s 2 da biste pronašli radijus.
- Evo primjera problema: Djevojka vozi vrtešku. Sjedalo je udaljeno 1 metar od središta kruga (radijusa). Ako se djevojka kreće po lučnoj putanji 1,5 metra (linearni pomak), koji je njen kutni pomak?
- Vaša jednadžba će izgledati ovako: = 1,5/1.
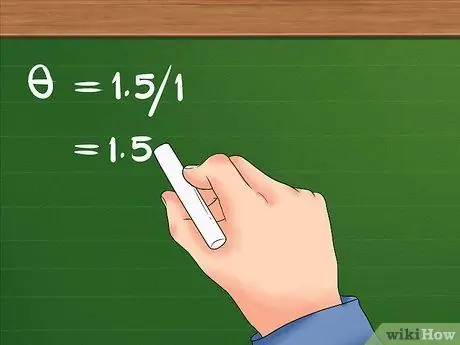
Korak 3. Podijelite linearni pomak s radijusom
Ova podjela će rezultirati kutnim pomakom objekta.
- Nakon dijeljenja 1,5 sa 1, rezultat je 1,5. Ugaoni pomak djevojčice je 1,5 radijani.
- Budući da kutni pomak mjeri koliko se objekt rotira od svog početnog položaja, treba ga mjeriti kao kut, a ne kao udaljenost. Radian je jedinica koja se koristi za mjerenje uglova.
5. dio od 5: Razumijevanje migracija
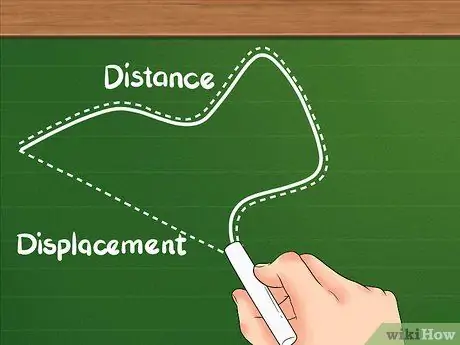
Korak 1. Znajte da udaljenost ima drugačiju definiciju od pomaka
Udaljenost pokazuje koliko je udaljenost prešao objekt.
- Udaljenost je često poznata kao skalarna veličina. Udaljenost prikazuje udaljenost koju je objekt prešao bez obzira na smjer objekta.
- Na primjer, ako hodate 2 koraka istočno, 2 koraka južno, 2 koraka zapadno, a zatim 2 koraka sjeverno, vratit ćete se u početni položaj. Iako ste prošli kroz ukupnu ocjenu razdaljina Samo 10 koraka dalje premjestiti 0 koraka dalje jer je vaša konačna lokacija ista kao i vaša početna lokacija (vaš put podsjeća na okvir).

Korak 2. Shvatite da je pomak razlika između dvije lokacije
Pomak nije ukupan zbir kretanja poput udaljenosti; prebacuje fokus na područje između vaše početne i krajnje lokacije.
- Pomak se naziva vektorska veličina i pokazuje promjenu položaja objekta uzimajući u obzir smjer kretanja objekta.
- Na primjer, hodate prema istoku 5 koraka. Ako se vratite 5 koraka prema zapadu, kretat ćete se u suprotnom smjeru od vaše izvorne lokacije. Iako ste prešli 10 koraka, vaš se položaj nije promijenio; vaš pomak je 0 koraka.

Korak 3. Zapamtite riječi naprijed i natrag kada pokušavate zamisliti pomak
Kretanje u suprotnom smjeru eliminira pomak objekta.
Zamislite fudbalskog trenera naprijed -nazad sa strane. Dok je vikao na igrače, nekoliko se puta pomaknuo s lijeva na desno. Ako ga promatrate dok se kreće s lijeva na desno, promatrate ukupnu udaljenost koju je prešao. Međutim, pretpostavimo da trener prestaje razgovarati s kvoterbekom sa strane. Ako se prije kretanja nalazi na drugom mjestu od početne lokacije, tada promatrate kretanje trenera

Korak 4. Znajte da se pomak mjeri ravnom, a ne kružnom stazom
Da biste pronašli pomak, morate pronaći najkraći i najefikasniji način za izračunavanje razlike između dvije točke.
- Kružni put će vas odvesti od početne lokacije do vaše konačne lokacije, ali to nije najkraći put. Da biste to lakše vizualizirali, zamislite da hodate ravno i nailazite na stup. Ne možete probiti ovaj stub, pa ga zaobiđite. Iako je vaš konačni položaj isti kao da ste probili stub, trebat će vam dodatni koraci da biste postigli taj cilj.
- Iako pomak predstavlja ravnu putanju, znajte da možete izmjeriti pomak objekta koji jeste trenutno kretati se kružnom putanjom. Taj pomak naziva se kutni pomak i može se izračunati pronalaženjem najkraćeg puta od početne lokacije do konačne lokacije.

Korak 5. Znajte da pomak može biti negativan, za razliku od udaljenosti
Ako se do vaše konačne lokacije dođe kretanjem u suprotnom smjeru od početnog smjera, vaš pomak je negativan.
- Na primjer, hodamo 5 koraka istočno, a zatim 3 koraka zapadno. Iako se računanjem krećete 2 koraka od početne lokacije, vaš pomak je -2 jer se krećete u suprotnom smjeru. Vaša udaljenost će uvijek biti pozitivna jer ne možete brojati unatrag u koracima, kilometrima itd.
- Negativno pomicanje ne znači da se pomak smanjuje. Negativno samo znači da je smjer suprotan.

Korak 6. Shvatite da ponekad udaljenost i pomak mogu biti isti
Ako hodate ravno 25 koraka i zaustavite se, udaljenost koju putujete bit će jednaka pomaku s vaše izvorne lokacije.
- Ovo se odnosi samo na to da se s jedne lokacije krećete pravocrtno s početne lokacije. Na primjer, živite u San Franciscu u Kaliforniji, a novi posao dobivate u Las Vegasu, Nevada. Morate se preseliti u Las Vegas da biste bili blizu posla. Ako uđete u avion koji leti ravno od San Francisca do Las Vegasa putovat ćete istom udaljenošću i pomakom x.
- Međutim, ako vozite od San Francisca do Las Vegasa, putovat ćete na udaljenost x, ali i na udaljenost y. Budući da vožnja automobila obično ima promjenjive smjerove (istočno od ove ceste, zapadno od te ceste), putovat ćete na veće udaljenosti od najkraće udaljenosti između dva grada.






