- Autor Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-15 08:10.
- Zadnja izmjena 2025-01-23 12:08.
Normalna sila je veličina sile potrebna za poništavanje drugih sila u bilo kojem scenariju. Najbolji način da ga pronađete ovisi o stanju objekta i varijablama koje imate. Nastavite čitati kako biste saznali više.
Korak
Metoda 1 od 5: Normalni stil u mirovanju
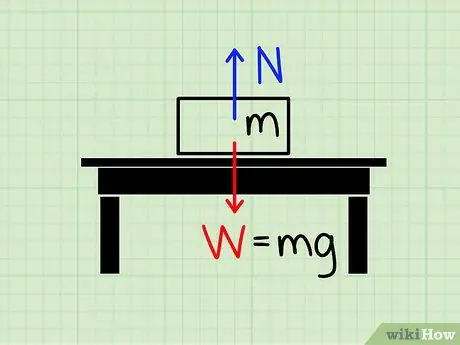
Korak 1. Shvatite značenje normalne sile
Normalna sila odnosi se na veličinu sile koja se koristi za poništavanje gravitacijske sile.
Zamislite blok koji miruje na stolu. Sila gravitacije povlači blok prema zemlji, ali očito postoji sila koja djeluje i sprječava blok da se zdrobi o stol i padne na tlo. Sila koja djeluje da zaustavi ovaj blok unatoč sili gravitacije naziva se normalni stil.
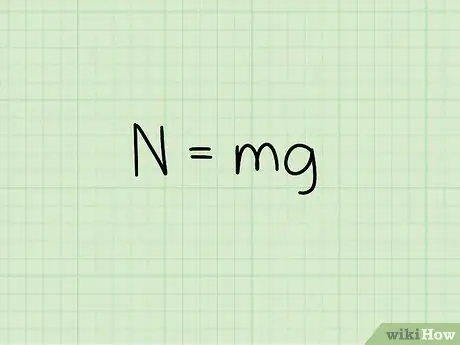
Korak 2. Upoznajte jednadžbu normalne sile na objekat koji miruje
Prilikom izračunavanja normalne sile objekta kada miruje na ravnoj površini, upotrijebite formulu: N = m * g
- U ovoj jednačini, N simbolizira normalan stil, m predstavlja masu objekta, i g predstavlja ubrzanje uslijed gravitacije.
- Za objekt koji miruje na ravnoj površini, bez djelovanja vanjske sile, normalna sila jednaka je težini objekta. Za održavanje objekta u mirovanju, normalna sila mora biti jednaka gravitacionoj sili koja djeluje na objekt. Gravitacijska sila koja djeluje na objekt je težina objekta ili masa objekta koja je puta ubrzana zbog gravitacije.
- Primjer: Nađite normalnu silu bloka mase 4,2 kg.
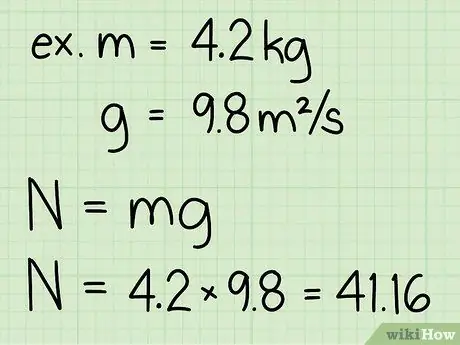
Korak 3. Pomnožite masu objekta i ubrzanje uslijed gravitacije
Ovo množenje će proizvesti težinu objekta, koja je naravno jednaka normalnoj sili objekta u mirovanju.
- Imajte na umu da je ubrzanje uslijed gravitacije na površini zemlje uvijek konstantno: g = 9,8 m/s2
- Primjer: težina = m * g = 4, 2 * 9, 8 = 41, 16

Korak 4. Zapišite svoje odgovore
Prethodni korak će riješiti problem, dajući vam odgovor.
Primjer: Normalna sila je 41, 16 N
Metoda 2 od 5: Normalna sila na nagnutoj ravni
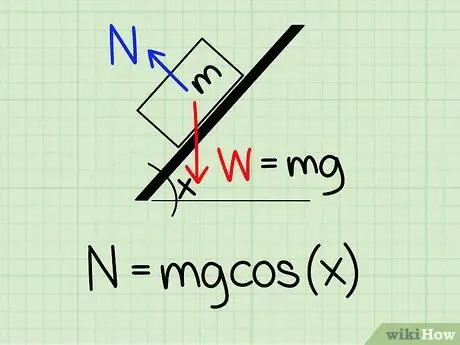
Korak 1. Koristite ispravnu jednadžbu
Da biste izračunali normalnu silu na objekt nagnut za određeni kut, morate koristiti formulu: N = m * g * cos (x)
- Za ovu jednačinu, N simbolizira normalan stil, m predstavlja masu objekta g predstavlja ubrzanje uslijed gravitacije, i x predstavlja koso ugao.
- Primjer: Pronađite normalnu silu bloka mase 4,2 kg, koji počiva na nagnutoj ravnini s nagibom od 45 stupnjeva.

Korak 2. Pronađite kosinus ugla
Kosinus ugla jednak je sinusu komplementarnog ugla ili susjednoj strani podijeljenoj hipotenuzom trokuta formiranog nagibom.
- Ova vrijednost se često određuje pomoću kalkulatora jer je kosinus bilo kojeg kuta uvijek konstantan, ali ga možete izračunati i ručno.
- Primjer: cos (45) = 0,71
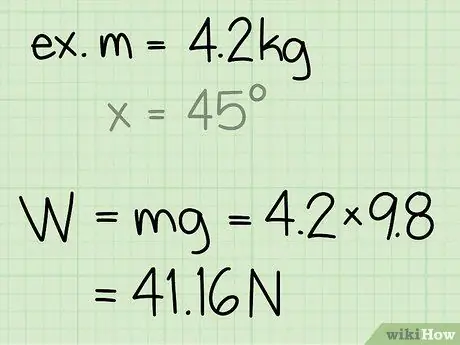
Korak 3. Pronađite težinu predmeta
Težina objekta jednaka je masi objekta puta ubrzanju uslijed gravitacije.
- Imajte na umu da je ubrzanje uslijed gravitacije na zemljinoj površini uvijek konstantno: g = 9,8 m/s2
- Primjer: težina = m * g = 4, 2 * 9, 8 = 41, 16
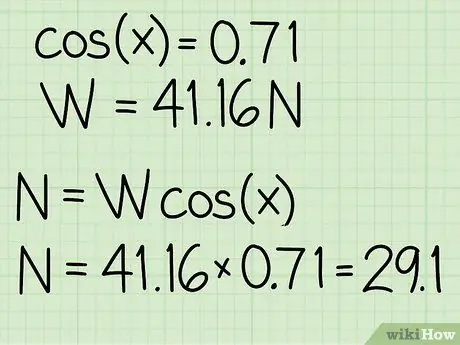
Korak 4. Pomnožite dvije vrijednosti
Da biste pronašli normalnu silu, morate pomnožiti težinu objekta s kosinusom kuta nagiba.
Primjer: N = m * g * cos (x) = 41, 16 * 0, 71 = 29, 1
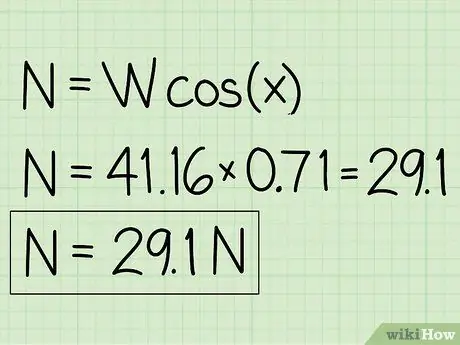
Korak 5. Zapišite svoje odgovore
Prethodni korak će riješiti problem i dati vaš odgovor.
- Imajte na umu da će, kada objekt miruje na nagibu, normalna sila biti manja od težine objekta.
- Primjer: Normalna sila je 29,1 N.
Metoda 3 od 5: Normalni stil sa vanjskim stilom nadole
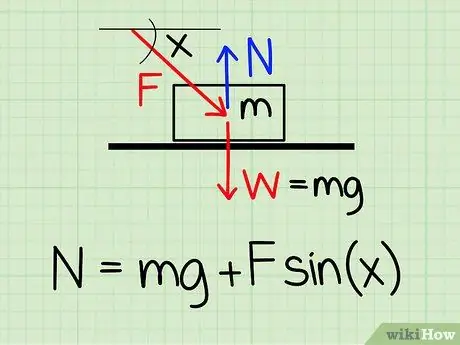
Korak 1. Koristite ispravnu jednadžbu
Za izračun normalne sile na objekt u mirovanju ako na objekt postoji vanjska sila prema dolje, upotrijebite jednadžbu: N = m * g + F * sin (x) '
- N simbolizira normalan stil, m predstavlja masu objekta g predstavlja ubrzanje uslijed gravitacije, F simbolizira vanjski stil i x predstavlja kut između objekta i smjera vanjske sile.
- Primjer: Pronađite normalnu silu objekta mase 4,2 kg ako ga osoba gurne pod kutom od 30 stupnjeva i silom od 20,9 N.
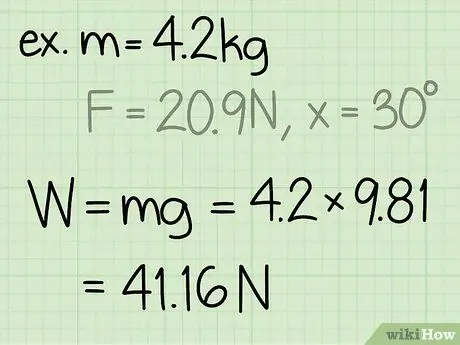
Korak 2. Pronađite težinu predmeta
Težina objekta jednaka je masi objekta puta ubrzanju uslijed gravitacije.
- Imajte na umu da je ubrzanje uslijed gravitacije na površini zemlje uvijek konstantno: g = 9,8 m/s2
- Primjer: težina = m * g = 4, 2 * 9, 8 = 41, 16
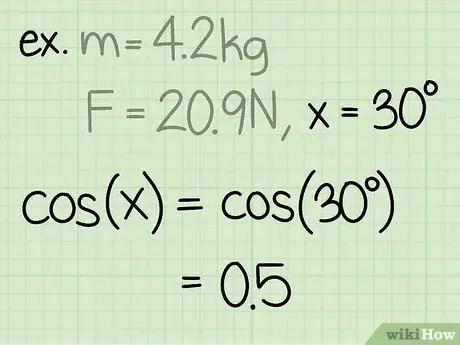
Korak 3. Pronađite sinus kuta
Sinus kuta izračunava se dijeljenjem stranice trokuta nasuprot kutu, hipotenuzom kuta.
Primjer: sin (30) = 0,5

Korak 4. Pomnožite sinus s vanjskom silom
Vanjska sila, u ovom primjeru, odnosi se na silu prema dolje koja udara u objekt.
Primjer: 0, 5 * 20, 9 = 10, 45
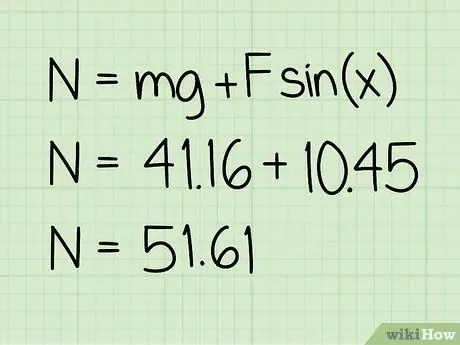
Korak 5. Dodajte ovu vrijednost težini
Ovaj zbroj će dati veličinu normalne sile koja djeluje.
Primjer: 10, 45 + 41, 16 = 51, 61
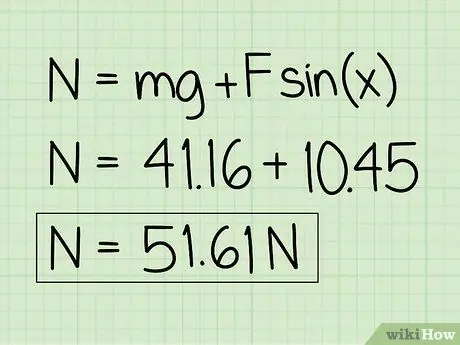
Korak 6. Zapišite svoje odgovore
Imajte na umu da će za objekt u mirovanju na koji djeluje vanjska sila prema dolje normalna sila biti veća od težine objekta.
Primjer: Normalna sila je 51,61 N
Metoda 4 od 5: Normalni stil s vanjskim stilom prema gore
Korak 1. Koristite ispravnu jednadžbu
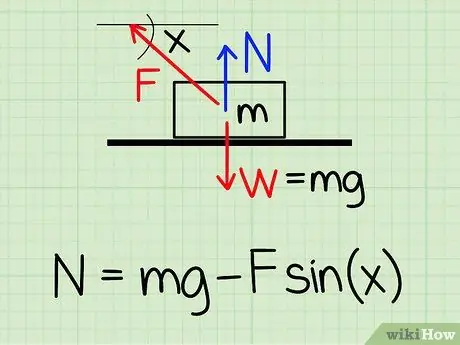
Za izračun normalne sile na objekt u mirovanju ako na objekt postoji vanjska sila prema gore, upotrijebite jednadžbu: N = m * g - F * sin (x) '
- N simbolizira normalan stil, m predstavlja masu objekta g predstavlja ubrzanje uslijed gravitacije, F simbolizira vanjski stil i x predstavlja kut između objekta i smjera vanjske sile.
- Primjer: Nađite normalnu silu bloka mase 4,2 kg, ako netko povuče blok prema gore pod kutom od 50 stupnjeva i silom od 20,9 N.

Korak 2. Pronađite težinu predmeta
Težina objekta jednaka je masi objekta puta ubrzanju uslijed gravitacije.
- Imajte na umu da je ubrzanje uslijed gravitacije na zemljinoj površini uvijek konstantno: g = 9,8 m/s2
- Primjer: težina = m * g = 4, 2 * 9, 8 = 41, 16
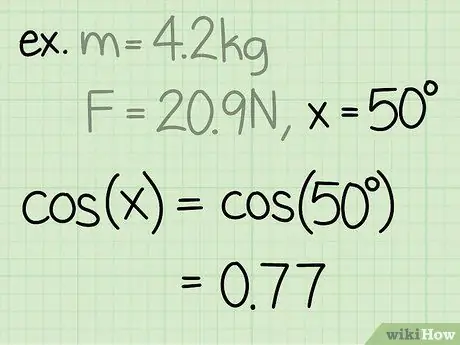
Korak 3. Pronađite sinus kuta
Sinus kuta izračunava se dijeljenjem stranice trokuta nasuprot kutu, hipotenuzom kuta.
Primjer: sin (50) = 0, 77

Korak 4. Pomnožite sinus s vanjskom silom
Vanjska sila se odnosi na silu prema gore koja udara u objekt, u ovom slučaju.
Primjer: 0,77 * 20, 9 = 16, 01
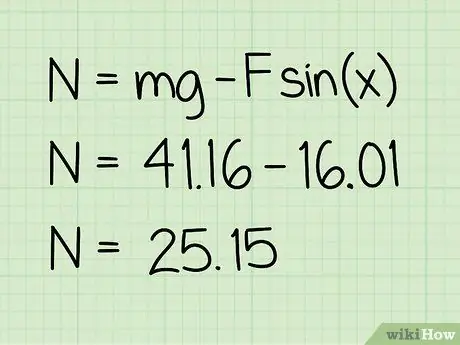
Korak 5. Oduzmite ovu vrijednost od težine
Oduzimanjem ćete dobiti veličinu normalne sile koja na nju djeluje.
Primjer: 41, 16 - 16, 01 = 25, 15
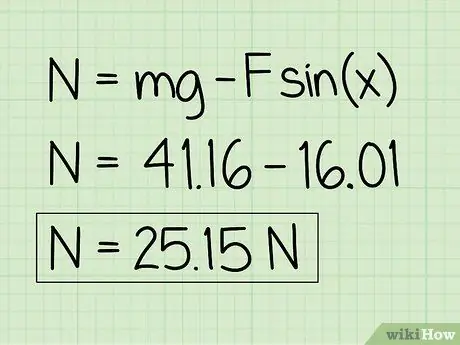
Korak 6. Zapišite svoje odgovore
Imajte na umu da na objekt u mirovanju djeluje vanjska sila prema gore, normalna sila bit će manja od težine objekta.
Primjer: Normalna sila je 25, 15 N
Metoda 5 od 5: Normalna sila i trenje

Korak 1. Znati osnovnu jednadžbu za kinetičko trenje
Kinetičko trenje ili trenje objekta u pokretu jednako je koeficijentu trenja puta normalnoj sili objekta. U obliku jednadžbe: f = * N
- U ovoj jednačini, f simboliziraju trenje, ️ predstavlja koeficijent trenja, i N predstavlja normalnu silu objekta.
- "Koeficijent trenja" je omjer sile trenja prema normalnoj sili, koja komprimira dvije suprotne površine.
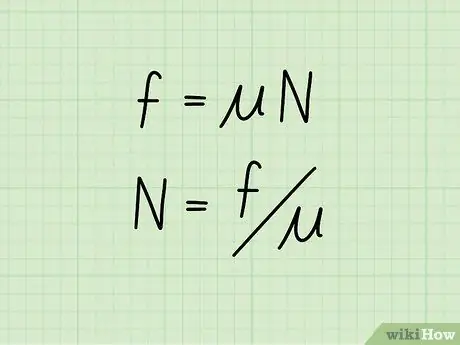
Korak 2. Postavite jednadžbu za izolaciju normalne sile
Ako znate vrijednost kinetičkog trenja objekta, kao i njegov koeficijent trenja, možete izračunati normalnu silu koristeći formulu: N = f /
- Obje strane izvorne jednadžbe podijeljene su sa ️, čime se izolira normalna sila s jedne strane, dok se s druge strane izračunava koeficijent trenja i kinetičko trenje.
- Primjer: Nađite normalnu silu bloka ako je koeficijent trenja 0,4, a veličina kinetičkog trenja 40 N.
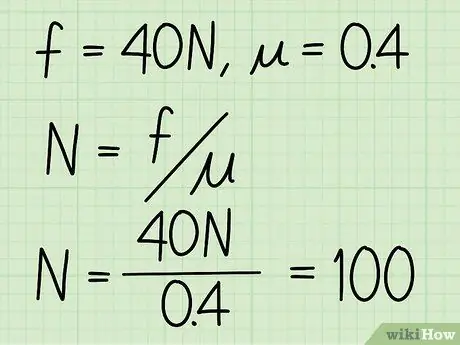
Korak 3. Podijelite kinetičko trenje s koeficijentom trenja
U osnovi, ovo je sve što trebate učiniti da biste utvrdili veličinu normalne sile.
Primjer: N = f / = 40 /0, 4 = 100
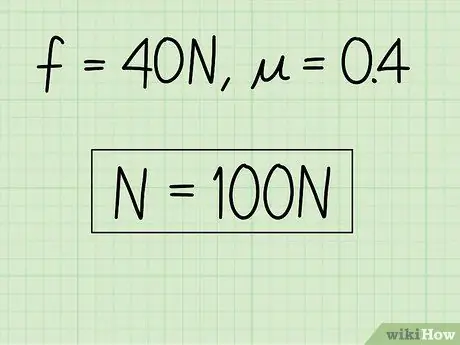
Korak 4. Zapišite svoje odgovore
Ako želite, svoj odgovor možete provjeriti tako da ga ponovo uključite u izvornu jednadžbu za kinetičko trenje. Ako to ne želite, riješili ste problem.






