Ukršteno množenje je način rješavanja jednadžbi koje uključuju varijablu od dva ekvivalentna razlomka. Varijabla je čuvar mjesta za nepoznatu količinu brojeva i unakrsnim množenjem pretvara se u jednostavnu jednadžbu, omogućavajući vam da pronađete vrijednost dotične varijable. Unakrsno množenje je vrlo korisno kada želite dovršiti poređenje. Evo kako to učiniti:
Korak
Metoda 1 od 2: Unakrsni proizvod jedne varijable
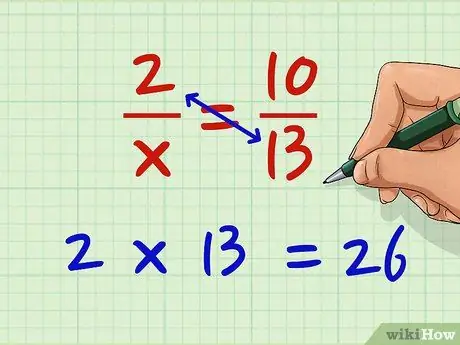
Korak 1. Pomnožite brojnik lijevog razlomka nazivnikom desnog razlomka
Recimo da želite riješiti jednadžbu 2/x = 10/13. Sada, pomnožite 2 sa 13,2 x 13 = 26.
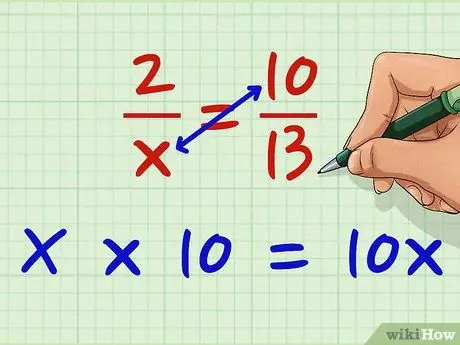
Korak 2. Pomnožite desni nazivnik s lijevim
Pomnožite x sa 10. X * 10 = 10x. Možete prvo prijeći ovaj odjeljak; nije važno sve dok množite oba brojnika s oba nazivnika dijagonalno.
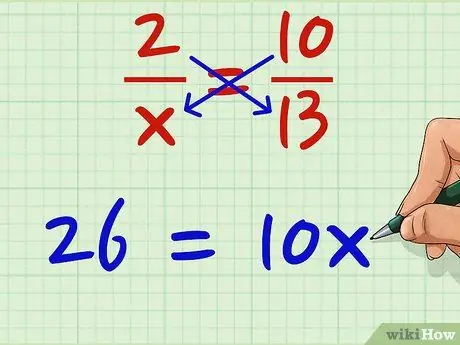
Korak 3. Neka dva proizvoda budu jednaka
26 je ekvivalentno 10x. 26 = 10x. Nije važno koja je desna ili lijeva; ako su jednaki, možete promijeniti njihovu lokaciju sve dok ih premještate odjednom.
Dakle, ako pokušate pronaći vrijednost x 2/x = 10/13, 2 * 13 = x * 10 ili 26 = 10x
Korak 4. Pronađite vrijednost varijable
Sada kada imate 26 = 10x, možete pokušati pronaći zajednički brojnik i podijeliti 26 i 10 na isti broj koji dijeli oba. Pošto su oba parna broja, možete ih podijeliti sa 2; 26/2 = 13 i 10/2 = 5. Ostatak je 13 = 5x. Sada, uzimajući samo x, podijelite obje strane jednadžbe sa 5. Dakle 13/5 = 5/5 ili 13/5 = x. Ako želite odgovor u decimalnom obliku, možete početi dijeljenjem obje strane jednadžbe s 10 kako biste dobili 26/10 = 10/10 ili 2,6 = x.
Metoda 2 od 2: Multivarijabilno unakrsno množenje
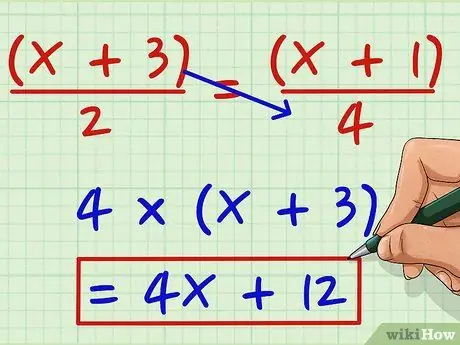
Korak 1. Pomnožite brojnik s lijeve strane nazivnikom s desne strane
Recimo da želite riješiti sljedeću jednadžbu: (x + 3)/2 = (x + 1)/4. Pomnožite (x + 3) sa 4 da biste dobili 4 (x + 3). Pomnožite sa 4 da biste dobili 4x + 12.
Korak 2. Pomnožite brojnik na desnoj strani s nazivnikom na lijevoj strani
Ponovite postupak sa druge strane. (x+1) x 2 = 2 (x+1). Pomnožite sa 2 da dobijete 2x + 2.
Korak 3. Učinite proizvod dviju jednakim i kombinirajte iste varijable
Sada je rezultat 4x + 12 = 2x + 2. Kombinujte promenljivu x i konstantu na drugoj strani jednačine.
- Dakle, kombinirajte 4x i 2x oduzimanjem 2x s obje strane. Oduzimanjem 2x od 2x ostavit će se ostatak 0. S lijeve strane 4x - 2x = 2x, tako da je ostatak 2x.
- Sada spojite 12 i 2 oduzimanjem 12 s obje strane. Oduzmite 12 od 12 na lijevoj strani i rezultat je 0, zatim oduzmite 12 od 2 na desnoj strani tako da je rezultat 2 -12 = -10.
- Ostatak je 2x = -10.
Korak 4. Završite
Sve što trebate učiniti je podijeliti obje strane jednadžbe sa 2. 2x/2 = -10/2 = x = -5. Nakon unakrsnog množenja, otkrićete da je x = -5. Možete se vratiti i provjeriti svoj rad unošenjem vrijednosti x, što je -5 kako biste bili sigurni da su obje strane jednake. Ispostavilo se da je ekvivalentno. Ako uključite -5 u originalnu jednadžbu, rezultat je -1 = -1.
Savjeti
- Imajte na umu da ako uključite različite brojeve (recimo 5) u istu jednadžbu, rezultat je 2/5 = 10/13. Čak i ako pomnožite lijevu stranu sa još 5/5, dobićete 10/25 = 10/13, što je očigledno pogrešno. Ovaj slučaj ukazuje na to da ste napravili unakrsnu grešku množenja.
- Svoj odgovor možete provjeriti uključivanjem rezultata u originalnu jednadžbu. Ako je jednadžba istinita tvrdnja, na primjer 1 = 1, vaš odgovor je tačan. Ako jednadžba postane lažna izjava, na primjer 0 = 1, pogriješili ste. Na primjer, uključite 2, 6 u jednadžbu tako da je 2/(2, 6) = 10/13. Pomnožite lijevu stranu sa 5/5 da biste dobili 10/13 = 10/13. Rezultat je tačna izjava, koja kada se pojednostavi postaje 1 = 1, pa je 2, 6 tačan odgovor.
