Matrica je pravokutni raspored brojeva, simbola ili izraza u redovima i stupcima. Da biste pomnožili matricu, morate pomnožiti elemente (ili brojeve) u prvom redu matrice s elementima u drugom redu matrice i zbrojiti proizvod. Matrice možete pomnožiti u samo nekoliko jednostavnih koraka koji zahtijevaju ispravno sabiranje, množenje i postavljanje rezultata.
Korak
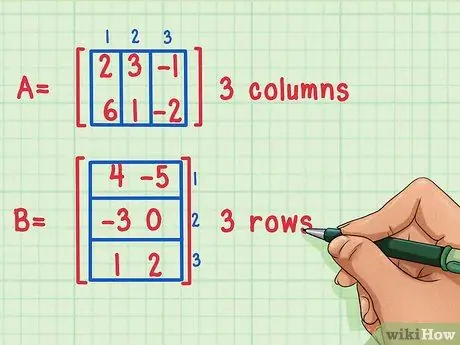
Korak 1. Uvjerite se da se matrice množe
Matricu možete pomnožiti samo ako je broj stupaca prve matrice jednak broju redova druge matrice.
Ove matrice se mogu pomnožiti jer prva matrica, matrica A, ima 3 stupca, dok druga matrica, matrica B, ima 3 reda
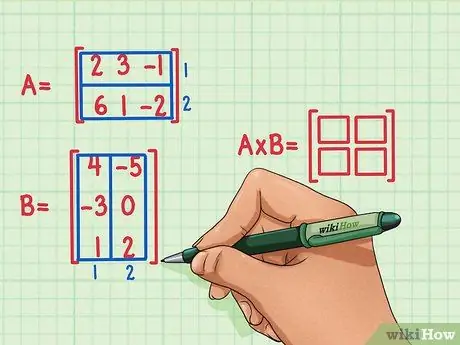
Korak 2. Označite dimenzije matričnog proizvoda
Kreirajte novu, praznu matricu koja će označavati dimenzije proizvoda dviju matrica. Matrica koja predstavlja umnožak matrice A i matrice B imat će isti broj redova kao prva matrica i isti broj stupaca kao druga matrica. Možete nacrtati prazna polja za prikaz broja redova i stupaca u ovoj matrici.
- Matrica A ima 2 reda, pa će rezultat množenja matrice imati 2 reda.
- Matrica B ima 2 kolone, pa će rezultat množenja matrice imati 2 kolone.
- Rezultat matričnog proizvoda će imati 2 reda i 2 kolone.
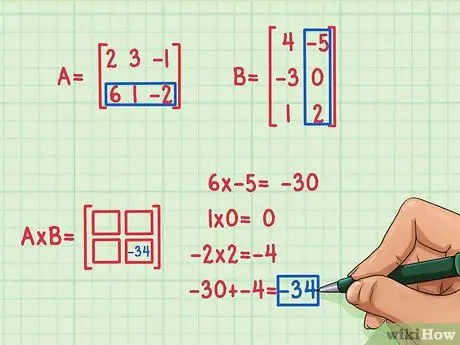
Korak 3. Pronađite rezultat prvog točkastog proizvoda
Da biste pronašli rezultat prvog točkastog proizvoda, morate pomnožiti prvi element u prvom redu s prvim elementom u prvom stupcu, drugi element u prvom redu s drugim elementom u prvom stupcu, a treći element u prvi red trećim elementom u prvoj koloni. Zatim zbrojite rezultate množenja da biste pronašli tačkasti proizvod (tačka).
Pretpostavimo da ste odlučili prvo izračunati elemente u drugom redu i drugoj koloni (dolje desno) proizvoda matrice. Evo kako to radite:
- 6 x -5 = -30
- 1 x 0 = 0
- -2 x 2 = -4
- -30 + 0 + (-4) = -34
-
Rezultat tačkastog proizvoda je -34 i ovaj rezultat je napisan u donjem desnom uglu matričnog proizvoda.
Kada pomnožite matricu, točkasti proizvod će biti upisan u položaj retka prve matrice i položaj kolone druge matrice. Na primjer, kada znate proizvod tačaka donjeg reda Matrice A i desne kolone Matrice B, odgovor, -34, upisuje se u donji red i desnu kolonu proizvoda matrice
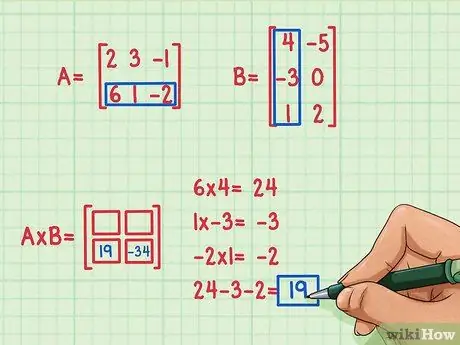
Korak 4. Pronađite rezultat proizvoda s drugom točkom
Pretpostavimo da želite pronaći pojam u donjem lijevom kutu matričnog proizvoda. Da biste pronašli ovaj pojam, trebate samo pomnožiti elemente u donjem redu prve matrice s elementima u prvom stupcu druge matrice, a zatim ih zbrojiti. Koristite istu metodu kao i množenje prvog reda i kolone - pronađite ponovo tačkasti proizvod (ne t)njegov.
- 6 x 4 = 24
- 1 x (-3) = -3
- (-2) x 1 = -2
- 24 + (-3) + (-2) = 19
- Rezultat tačkastog proizvoda je -19 i ovaj rezultat je napisan u donjem lijevom kutu matričnog proizvoda.
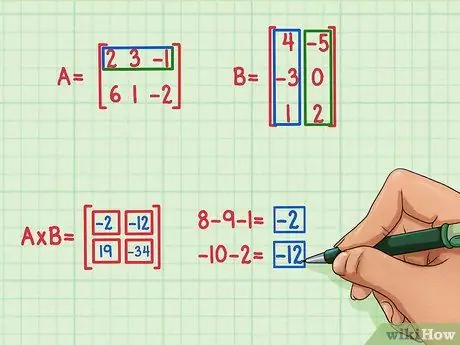
Korak 5. Pronađite druga dva proizvoda sa tačkama
Da biste pronašli pojam u gornjem lijevom kutu matričnog proizvoda, počnite tako što ćete pronaći proizvod sa tačkama gornjeg reda Matrice A i lijeve kolone Matrice B. Evo kako to radite:
- 2 x 4 = 8
- 3 x (-3) = -9
- (-1) x 1 = -1
- 8 + (-9) + (-1) = -2
-
Rezultat tačkastog proizvoda je -2 i ovaj rezultat je napisan u gornjem lijevom kutu matričnog proizvoda.
Da biste pronašli izraz u gornjem desnom kutu matričnog proizvoda, samo potražite proizvod s točkama gornjeg reda Matrice A i desne kolone Matrice B. Evo kako to radite:
- 2 x (-5) = -10
- 3 x 0 = 0
- (-1) x 2 = -2
- -10 + 0 + (-2) = -12
- Točkasti proizvod je -12 i ovaj rezultat je napisan u gornjem desnom kutu matričnog proizvoda.
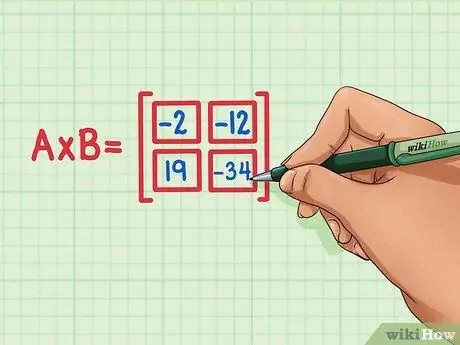
Korak 6. Uvjerite se da su proizvodi sa četiri tačke na ispravnom mjestu u matričnom proizvodu
19 mora biti dolje lijevo, -34 mora biti dolje desno, -2 mora biti gore lijevo, a -12 mora biti gore desno.
Savjeti
- Korištenje segmenata linija, a ne korištenje linija, može dati pogrešan odgovor. Ako linija koja predstavlja red zahtijeva proširenje za prelazak preko stupca, onda ga produžite! Ovo je samo tehnika vizualizacije koja će vam olakšati da znate koje retke i stupce koristiti za rad sa svakim elementom proizvoda.
- Umnožak dviju matrica proizvest će broj redova jednak broju redova prve matrice i broj stupaca jednak broju kolona druge matrice.
- Zapišite svoj iznos. Množenje matrica uključuje mnogo izračunavanja i vrlo je lako zaobići i zaboraviti koji broj množite.
