Pomoću Spearmanovog koeficijenta korelacije ranga možemo identificirati da li dvije varijable imaju monotonu funkciju (to jest, kada se jedan broj poveća, i drugi će se povećati, ili obrnuto). Da biste izračunali Spearmanov koeficijent korelacije ranga, morate rangirati i uporediti skupove podataka da biste pronašli d2, a zatim unesite podatke u standardnu ili pojednostavljenu formulu koeficijenta korelacije ranga po Spearmanu. Ove koeficijente možete izračunati i pomoću Excel formula ili naredbe R.
Korak
Metoda 1 od 3: Ručni način
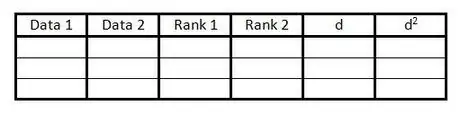
Korak 1. Kreirajte tabelu
Tablica se koristi za uključivanje svih podataka potrebnih za izračun Spearmanovog koeficijenta korelacije ranga. Potrebna vam je ovakva tablica:
- Napravite 6 stupaca s naslovima, kao u primjeru.
- Pripremite onoliko praznih redova koliko ima i parova podataka.
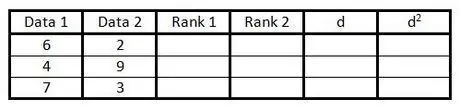
Korak 2. Popunite prve dvije kolone parovima podataka
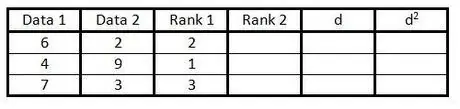
Korak 3. Unesite rangiranje prve kolone grupa podataka u treću kolonu od 1 do n (broj podataka)
Dajte ocjenu 1 za najnižu vrijednost, ocjenu 2 za sljedeću najnižu vrijednost itd.
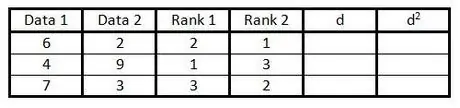
Korak 4. U četvrtoj koloni učinite isto kao u koraku 3, ali za rangiranje podataka u drugoj koloni
-
Mean_742 Ako postoje dva (ili više) podataka koji imaju istu vrijednost, izračunajte prosječnu ocjenu podataka, a zatim ih unesite u tablicu na osnovu ove prosječne vrijednosti.
U primjeru s desne strane postoje dvije vrijednosti 5 na ocjenama 2 i 3. Budući da postoje dvije petice, pronađite prosjek ocjena. Prosjek 2 i 3 je 2,5, pa unesite vrijednost ocjene 2,5 za obje vrijednosti 5.
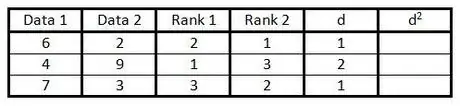
Korak 5. U koloni "d" izračunajte razliku između dva broja u koloni ranga
To jest, ako je jedna kolona rangirana 1, a druga kolona 3, razlika je 2. (Znak nije bitan, jer je sljedeći korak kvadratovanje vrijednosti.)
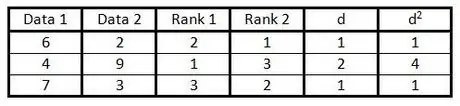
Korak 6. Uokvirite svaki broj u kolonu "d", a rezultat upišite u kolonu "d"2".
Korak 7. Dodajte sve podatke u kolonu d2".
Rezultat je d2.
Korak 8. Odaberite jednu od sljedećih formula:
-
Ako nijedna ocjena nije ista kao u prethodnom koraku, unesite ovu vrijednost u pojednostavljenu formulu koeficijenta korelacije ranga Spearmana
Step8_271 i zamijenite "n" s brojem parova podataka da biste dobili rezultat.
Step9_402 -
Ako u prethodnom koraku postoji sličan rang, upotrijebite standardnu formulu Spearmanov koeficijent korelacije ranga:
Spearman
Korak 9. Tumačite rezultate
Vrijednost može varirati između -1 i 1.
- Ako je vrijednost blizu -1, korelacija je negativna.
- Ako je vrijednost blizu 0, nema linearne korelacije.
- Ako je vrijednost blizu 1, korelacija je pozitivna.
Metoda 2 od 3: Korištenje programa Excel
Korak 1. Kreirajte novu kolonu za podatke zajedno sa njihovim rangiranjem
Na primjer, ako su vaši podaci u stupcu A2: A11, upotrijebite formulu "= RANK (A2, A $ 2: A $ 11)" i kopirajte ih sve dok ne pokriju sve stupce i retke.
Korak 2. Promijenite istu ocjenu kao što je opisano u koracima 3 i 4 metode 1
Korak 3. U novoj ćeliji izračunajte korelaciju između dva stupca ranga s formulom "= CORREL (C2: C11, D2: D11)"
U ovom primjeru, C i D se odnose na kolonu u kojoj se nalazi rang. Nova ćelija će biti ispunjena Spearmanovom korelacijom ranga.
Metoda 3 od 3: Korištenje R
Korak 1. Prvo instalirajte program R ako ga već nemate
(Pogledajte
Korak 2. Spremite podatke u CSV obrazac, stavite podatke za koje želite da pronađu korelaciju u prve dvije kolone
To možemo učiniti pomoću izbornika "Spremi kao".
Korak 3. Otvorite R Editor
Ako radite s terminala, samo pokrenite R. Ako radite s radne površine, kliknite ikonu R.
Korak 4. Unesite sljedeću naredbu:
- d <- read.csv ("NAME_OF_YOUR_CSV.csv") i pritisnite Enter.
- cast (čin (d [, 1]), čin (d [, 2]))
Savjeti
Podaci se moraju sastojati od najmanje 5 parova kako bi se mogao vidjeti trend (broj podataka je 3 para u primjeru samo radi pojednostavljenja proračuna.)
Upozorenje
- Spearmanov koeficijent korelacije ranga samo identificira jačinu korelacije tamo gdje podaci dosljedno rastu ili padaju. Ako postoji još jedan trend u podacima, korelacija Spearmanovog ranga no će pružiti tačan prikaz.
- Ova se formula temelji na pretpostavci da ne postoje jednake ocjene. Kada postoji isti rang kao u primjeru, trebali bismo koristiti ovu definiciju: koeficijent korelacije trenutka množenja po rangu.
