- Autor Jason Gerald gerald@how-what-advice.com.
- Public 2024-02-01 14:12.
- Zadnja izmjena 2025-01-23 12:08.
Postupak određivanja kvadratnog inča (napisan u2) u svim su područjima dvodimenzionalne figure obično prilično jednostavne. U najjednostavnijem slučaju, kada je lik kvadrat ili četverokut, površina u inčima na kvadrat može se dobiti pomoću formule dužina × širina.
Područja drugih oblika ravnina (krugovi, trokuti itd.) Mogu se izračunati pomoću različitih matematičkih formula. Također možete napraviti jednostavnu konverziju stopa na kvadrat ili centimetara na kvadrat od centimetara na kvadrat, ako je potrebno.
Korak
Metoda 1 od 3: Određivanje kvadratnih inča na kvadratu ili kvadratu
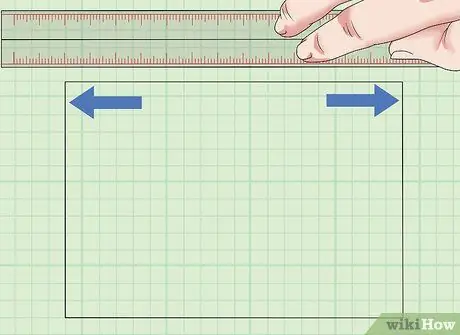
Korak 1. Odredite dužinu površine koju ćete mjeriti
Kvadrati i pravokutnici imaju 4 ravne stranice. Kvadrat ima četiri stranice iste dužine, dok su u pravokutniku samo suprotne stranice iste dužine. Izmjerite jednu stranu kvadrata ili pravokutnika kako biste saznali vrijednost dužine.
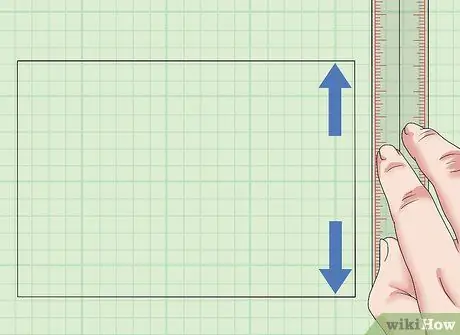
Korak 2. Odredite širinu područja koje ćete mjeriti
Zatim izmjerite jednu od strana pored prethodno izmjerene strane. Ova strana treba da se sastane sa prvom stranom pod uglom od 90 stepeni. Ovo je širina vašeg kvadrata ili pravokutnika.
Budući da su sve četiri stranice kvadrata iste dužine, rezultirajuća "dužina" bit će jednaka mjeri "širine". Dakle, obično za kvadrat trebate izmjeriti samo jednu stranu
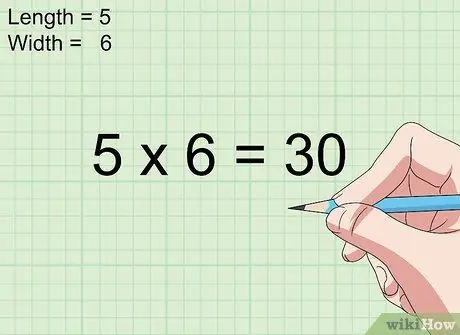
Korak 3. Pomnožite dužinu i širinu
Jednostavno pomnožite mjere duljine i širine kako biste odredili površinu kvadrata ili pravokutnika u inčima na kvadrat.
- Na primjer, recimo da problem traži površinu pravokutnika dugačkog 4 inča i širokog 3 inča. U ovom slučaju površina pravokutnika je 4 x 3 = 12 inča na kvadrat.
- Opet, sve stranice kvadrata imaju istu dužinu stranica. Dakle, trebate samo izmjeriti jednu stranu i pomnožiti je sa samim brojem (poznatim i kao "kvadratura" ili prema stepenu dva) da biste dobili površinu u inčima na kvadrat.
Metoda 2 od 3: Određivanje kvadratnih inča na drugim ravnim oblicima
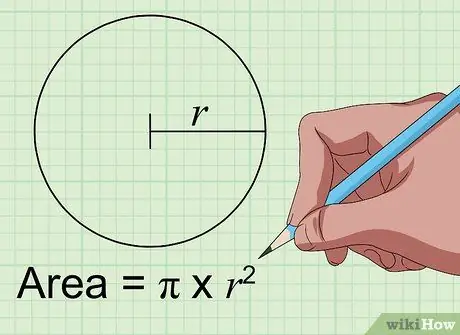
Korak 1. Pronađite površinu kruga koristeći formulu Površina = pi × r2.
Da biste pronašli površinu kruga u inčima na kvadrat, trebate znati samo udaljenost od središta kruga do njegovih stranica u inčima. Ova udaljenost naziva se "radijus" kruga. Ako ste ga dobili, jednostavno unesite broj u varijablu "r" u gornjoj formuli. Pomnožite sa samim brojem, a zatim pomnožite s konstantom pi (3, 1415926 …) da biste dobili površinu kruga u inčima na kvadrat.
Dakle, krug s radijusom od 4 inča ima površinu od 50,27 inča na kvadrat, što je umnožak 3,14 x 16
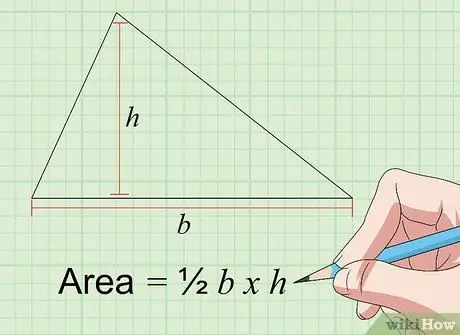
Korak 2. Pronađite površinu trokuta koristeći formulu Površina = 1/2 a × t
Područje trokuta u inčima na kvadrat može se pronaći množenjem osnove ("a") i visine ("t"), a oba su u inčima. Osnova trokuta je dužina jedne njegove stranice, dok je "visina" trokuta udaljenost od stranice "osnove" do ugla trokuta nasuprot njemu pod kutom od 90 stupnjeva. Površina trokuta može se izračunati ako znate dužine stranica osnove i visine tri stranice i kutove nasuprot njima.
Dakle, ako odaberete stranu koja je 4 inča duga kao osnova, a visina te stranice baze je 3 inča, površina trokuta je 2 x 3 = 6 inča na kvadrat
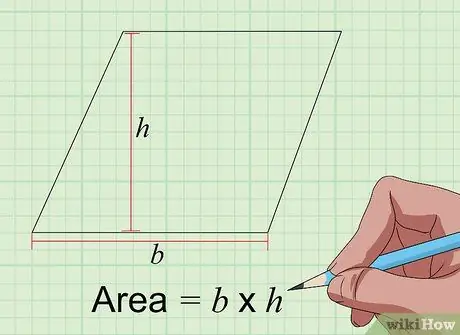
Korak 3. Pronađite površinu paralelograma s formulom Površina = a × t
Paralelogram je sličan pravokutniku, ali se stranice ne spajaju pod kutom od 90 stupnjeva. Međutim, način da se pronađe površina paralelograma u inčima na kvadrat isti je kao i u pravokutniku, množenjem osnove s visinom u inčima. Baza je dužina jedne od njegovih stranica, dok je visina udaljenost od stranice baze do suprotne strane pod uglom od 90 stepeni.
Stoga, ako je dužina odabrane strane 5 inča, a nakon mjerenja visine dugačka je 4 inča, površina je 5 x 4 = 20 inča na kvadrat
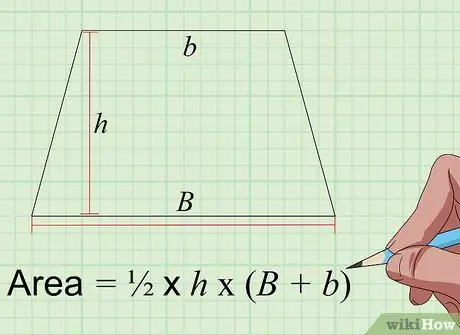
Korak 4. Pronađite površinu trapeza koristeći formulu Površina = 1/2 × t × (A+a)
Trapez je četverostrani ravni oblik s jednim parom paralelnih stranica i drugim neparalelnim stranicama. Da biste izračunali površinu trapeza u inčima na kvadrat, morate znati 3 mjerenja u inčima, dužinu duge paralelne stranice ("A"), kraću paralelnu stranu ("a") i visinu trapeza ("t"), odnosno udaljenost između dvije paralelne stranice mjereno u kutovima od 90 stupnjeva. Dodajte duljine dviju paralelnih stranica, pomnožite s visinom, a zatim podijelite s dva da biste dobili površinu trapeza u inčima na kvadrat.
Na primjer, ako su paralelne stranice trapeza dugačke 6 inča, kratke paralelne stranice su 4 inča, a visina 5 inča, površina je x 5 x (6+4) = 25 kvadratnih inča
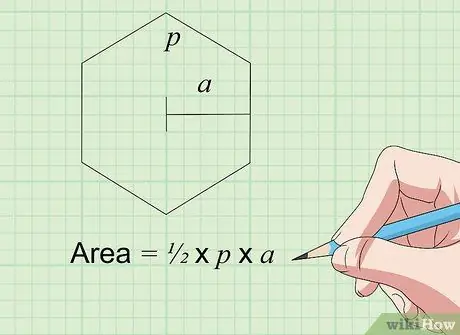
Korak 5. Pronađite površinu šesterokuta (šesterokuta) s formulom Površina = × K × s
Ova formula funkcionira za sve pravilne šesterokute, koji su ravni oblici koji imaju 6 jednakih stranica i 6 jednakih kutova. K je obod ili dužina stranice 6 (6 x s) za pravilan šesterokut. Varijabla a predstavlja apotemu, koja je dužina od središta šesterokuta do jedne od njegovih stranica (sredina stranice između dva ugla). Pomnožite i podijelite rezultat kako biste pronašli površinu šesterokuta.
Dakle, ako je šesterokut sa svih šest stranica dugačak 4 inča (što znači K = 6 x 4 = 24), a apotem je dugačak 3,5 inča, površina je x 24 x 3,5 = 42 kvadratna inča
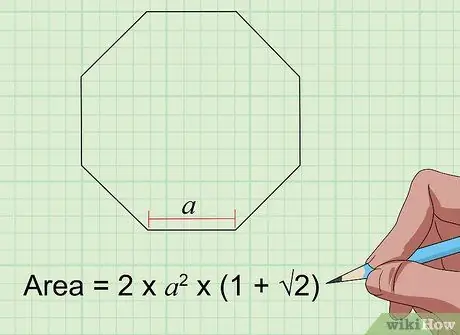
Korak 6. Pronađite površinu osmougaonika s formulom Površina = 2s² × (1 + 2)
Za pravilan osmougao (koji ima 8 jednakih stranica i 8 uglova), morate znati samo dužinu jedne stranice („s“u formuli) da biste pronašli površinu. Uključite vrijednosti u formulu i razradite ih kako biste dobili površinu osmerokuta.
Ako vaš pravilan osmerokut ima bočnu dužinu od 4 inča, njegova površina je 2 (16) x (1 + 1, 4) = 32 x 2,4 = 76,8 kvadratnih inča
Metoda 3 od 3: Pretvaranje drugih jedinica u kvadratne inče

Korak 1. Promijenite veličinu u inče prije izračuna
Da biste dobili konačan odgovor u inčima na kvadrat, preporučujemo da sve vrijednosti koje treba izračunati pretvorite u inče (poput dužine, visine ili apoteme). Stoga, ako su stranice kvadrata svaka 1 stopa, pretvorite ih u 12 inča prije izračunavanja površine. Za pretvaranje u inče obično se koriste sljedeći faktori konverzije:
- 1 stopa = 12 inča
- 1 jarda = 36 inča
- 1 centimetar = 0,3937 inča
- 1 metar = 39.3701 inča
- 1 milimetar = 0,0394 inča
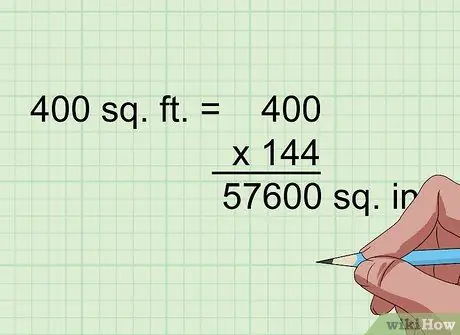
Korak 2. Pomnožite sa 144 da biste kvadratne stope pretvorili u kvadratne inče
1 stopa na kvadrat je 1 stopa na kvadrat (1 stopa puta 1 stopa); što znači da je 12 inča na kvadrat jednako 12 inča puta 12 inča, što čini 144 inča na kvadrat. Dakle, ako ravni oblik ima površinu u stopama na kvadrat, jednostavno ga pomnožite sa 144 da biste ga pretvorili u centimetre na kvadrat.
Na primjer, 400 stopa na kvadrat = 400 x 144 = 57 600 inča na kvadrat
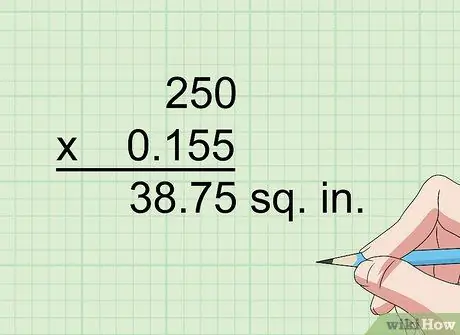
Korak 3. Pomnožite sa 0,155 da biste kvadratne centimetre pretvorili u kvadratne inče
Jedan centimetar jednak je 0,394 inča, a 0,394 na kvadrat (0,394 x 0,394) jednako je 0,155. Tako, na primjer, ako trebate pretvoriti 250 centimetara na kvadrat u inčeve na kvadrat, pomnožite 250 sa 0,155 da biste dobili 38,75 inča na kvadrat.






