- Autor Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-16 19:14.
- Zadnja izmjena 2025-01-23 12:08.
Brzina je proračun koliko se brzo nešto kreće u jednom trenutku. Ako ste ikada pogledali brzinomjer automobila u pokretu, vidjet ćete brojanje brzina - što se igla više kreće, to je veća brzina vozila. Postoji nekoliko načina za izračunavanje brzine, ovisno o vrsti informacija koje imate. Općenito, formula brzina = udaljenost/vrijeme (ili k = j/w) je najlakši način za izračunavanje brzine.
Korak
Metoda 1 od 3: Korištenje standardnih formula za izračunavanje brzine

Korak 1. Pronađite udaljenost koju je objekt prešao
Osnovna formula koju većina ljudi koristi za pronalaženje brzine nečega vrlo je laka za korištenje. Prije svega, morate znati "koliko je udaljenosti prešao izmjereni objekt". Drugim riječima, koja je udaljenost između početne i krajnje tačke objekta?
Ovu formulu je lakše razumjeti kroz primjer. Recimo da automobilom putujemo do igrališta na "161 kilometar". U nekoliko koraka ove podatke možemo upotrijebiti za dovršetak izračuna formule

Korak 2. Odredite koliko je vremena potrebno objektu da pređe tu udaljenost
Sljedeća informacija koja vam je potrebna je koliko je potrebno objektu da dosegne određenu udaljenost. Drugim riječima, koliko je potrebno da se objekt pomakne od početne do krajnje točke?
U ovom primjeru, recimo da objektu treba cca. dva sata da dođete do odredišta.

Korak 3. Podijelite udaljenost s vremenom potrebnim za pronalaženje brzine objekta
Ove dvije informacije trebaju vam samo da biste znali brzinu objekta. Udaljenost do vremena jednaka je brzini objekta.
U ovom primjeru, 161 kilometar/2 sata = 80,5 kilometara na sat.

Korak 4. Ne zaboravite korištenu jedinicu
Vrlo je važno koristiti točne jedinice u svom odgovoru (poput kilometara na sat itd.) Bez ovih jedinica, ljudima je vrlo teško razumjeti značenje vašeg odgovora. Također možete izgubiti bodove ako koristite pogrešnu jedinicu prilikom izvršavanja školskih zadataka.
Jedinica brzine je jedinica udaljenosti do jedinice vremena. Na primjer, budući da mjerimo udaljenost u kilometrima i vrijeme u satima, korištene su jedinice kilometara/sat (ili kilometara na sat).
Metoda 2 od 3: Rješavanje težih proračuna

Korak 1. Pronađite nekoliko različitih varijabli za rješavanje problema udaljenosti i vremena
Kad shvatite osnovnu formulu za brzinu, možete je koristiti za obavljanje drugih izračuna, a ne za brzinu. Na primjer, ako isprva znate samo brzinu objekta i još jednu varijablu, možete preurediti gornju formulu kako biste pronašli nepoznate informacije.
-
Na primjer, recimo da znamo da voz vozi četiri sata brzinom od 20 kilometara na sat, ali ne znamo koliko je daleko putovao. Da bismo to saznali, formulu možemo preurediti na sljedeći način:
-
- brzina = udaljenost/vrijeme
- brzina × vrijeme = (udaljenost/vrijeme) × vrijeme
- brzina × vrijeme = udaljenost
- 20 km/sat × 4 sata = udaljenost = 80 kilometara
-

Korak 2. Pretvorite jedinice koje koristite prema potrebi
Ponekad možete izračunati brzinu pomoću određene jedinice, ali je trebate pretvoriti u drugu jedinicu. U ovom slučaju morate koristiti faktor konverzije da biste dobili odgovor prema ispravnim jedinicama. Da biste to učinili, jednostavno napišite odnos između jedinica u obliku razlomka i pomnožite. Prilikom množenja obrnite razlomak prema potrebi kako biste uklonili neželjene jedinice. Ova metoda je mnogo lakša nego što zvuči!
-
Na primjer, recimo da nam je u gore navedenom primjeru odgovor potreban u miljama umjesto u kilometrima. Jedna milja jednaka je oko 1,6 kilometara. Dakle, pretvorbu možemo izvršiti na sljedeći način:
-
- 80 kilometara × 1 milja/1,6 kilometara = 50 milja
-
- Upamtite, budući da se kilometri pojavljuju na dnu razlomka, oni uklanjaju kilometre iz prethodnog odgovora, pa konačni rezultat koristi milje.
- Ova web stranica nudi značajke konverzije za većinu najčešće korištenih jedinica.

Korak 3. Zamijenite varijablu "distance" formulom udaljenosti po potrebi
Objekti se ne kreću uvijek ravno, glatko. Ako je to istina, možda nećete moći jednostavno unijeti numeričku vrijednost kao jedinicu udaljenosti u standardnu formulu brzine. Međutim, možda ćete morati zamijeniti slovo j u formuli k = j/w formulom koja podsjeća na udaljenost koju je objekt prešao.
-
Na primjer, recimo da se avion rotira kroz zrak na udaljenosti od 20 milja 5 puta. Avion je rundu završio za pola sata. U ovom primjeru još uvijek moramo pronaći ukupnu udaljenost koju je avion prešao prije nego što možemo odrediti njegovu brzinu. U ovoj formuli možemo umjesto formule j izračunati udaljenost oko kruga (udaljenost oko nje) umjesto j. Ova formula je opseg = 2πr gdje je r = polumjer kruga. Evo kako to riješiti:
-
- k = (2 × × r)/w
- k = (2 × × 10) /0,5
- k = 62,83/0,5 = 125,66 milja/sat
-

Korak 4. Shvatite da k = j/w daje prosječnu brzinu
Laka i jednostavna formula koju koristimo za pronalaženje brzine ima jedan nedostatak. Dobivena vrijednost tehnički je prosječna brzina. To znači da formula pretpostavlja da objekt koji mjerite koristi istu brzinu dok se kreće. Kao što ćemo vidjeti u nastavku, pronalaženje brzine objekta u jednom trenutku bit će mnogo teže.
Kako biste ilustrirali ovu razliku, zamislite kada ste zadnji put putovali automobilom. Malo je vjerojatno da ćete putovati istom brzinom kojom putujete. Međutim, obično ćete započeti svoje putovanje malom brzinom i usput postupno povećavati brzinu, zaustavljajući se zbog crvenih svjetala, gužvi u prometu itd. Ako koristite standardnu formulu brzine za pronalaženje brzine tokom putovanja, promjene te brzine se ne mogu otkriti. Međutim, dobit ćete odgovor koji prikazuje prosječnu brzinu svih razlika u brzini koje putujete
Metoda 3 od 3: Izračunavanje trenutne brzine
Bilješka:
Ovaj odjeljak koristi tehnike koje su manje poznate ljudima koji nikada nisu proučavali račun. Za pomoć pročitajte naše članke o računanju.
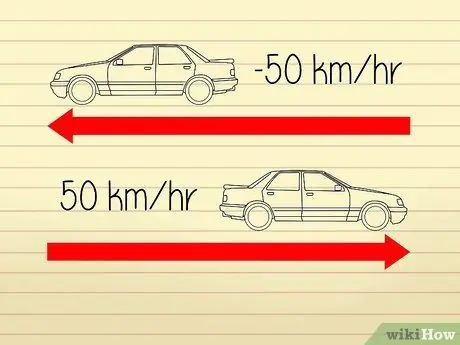
Korak 1. Shvatite da je brzina definirana kao stopa ubrzanja
Proračuni brzine na visokom nivou prilično su zbunjujući jer matematičari i naučnici koriste različite definicije za opisivanje "brzine" i "ubrzanja". Ubrzanje ima dvije komponente: "brzinu" i "smjer". Brzina je jednaka brzini objekta. Promjena smjera uzrokovat će promjenu ubrzanja, ali ne i promjenu brzine.
- Na primjer, recimo da se dva automobila kreću u suprotnim smjerovima. Brzinomjeri na oba automobila prikazuju brojku od 50 km/h pa se obojica kreću istom brzinom. Međutim, budući da se automobili udaljavaju jedan od drugog, možemo reći da jedan od automobila ima "ubrzanje" od -50 km/h, dok drugi ima "ubrzanje" od 50 km/h.
- Baš kao i proračuni trenutne brzine, možete izvesti i proračune trenutnog ubrzanja.

Korak 2. Koristite apsolutne vrijednosti za mjerenje negativnog ubrzanja
Objekt može imati negativnu brzinu ubrzanja (ako se kreće u negativnom smjeru u odnosu na drugi objekt). Međutim, nema negativne brzine. Dakle, u ovom slučaju apsolutna vrijednost kursa označava brzinu objekta.
Iz tog razloga, u gore navedenom primjeru, oba automobila imaju brzinu od 50km/h.
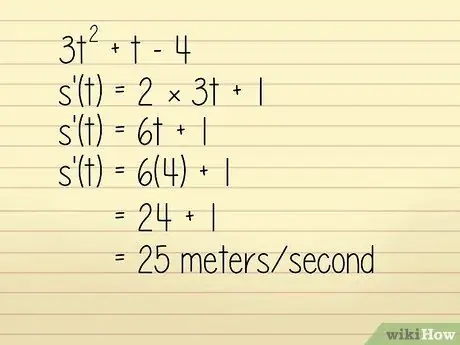
Korak 3. Uzmite derivaciju položaja funkcije
Ako imate funkciju k (w) koja prikazuje položaj objekta bez potrebe za izračunavanjem vremena, derivacija k (w) će pokazati ubrzanje bez potrebe za mjerenjem vremena. Samo uključite vrijednost vremena u ovu formulu tako da se varijabla w (ili bilo koja druga vrijednost vremena koja se koristi) ubrza u skladu s tim vremenom. Odavde možete lako pronaći brzinu objekta.
-
Na primjer, recimo da je položaj objekta u jednom metru opisan u jednadžbi 3q2 + w - 4 gdje je w = vrijeme u sekundama. Želimo znati brzinu objekta pri w = 4 sekunde. U ovom slučaju to možete riješiti na sljedeći način:
-
- 3w2 +w - 4
- k '(w) = 2 × 3w + 1
- k '(w) = 6w + 1
-
-
Sada unosimo w = 4:
-
- k '(w) = 6 (4) + 1 = 24 + 1 = 25 metara u sekundi. Tehnički je ovo proračun ubrzanja, ali budući da je pozitivan i smjer nije spomenut u pitanju, možemo ga koristiti za pronalaženje brzine.
-

Korak 4. Uzmite funkciju integralnog ubrzanja
Ubrzanje je način mjerenja promjene ubrzanja objekta tijekom vremena. Ova je tema previše složena da bi se mogla u potpunosti objasniti u ovom članku. Međutim, korisno je napomenuti da kada imate funkciju a (w) koja predstavlja ubrzanje u odnosu na vrijeme, integral a (w) će vratiti rezultat ubrzanja na temelju tog vremena. Upamtite, vrlo je korisno znati početno ubrzanje objekta kako biste mogli definirati konstantu tog rezultata iz beskonačnog integrala.
-
Na primjer, recimo da objekt ima konstantno ubrzanje (u m/s2 kao rezultat a (w) = -30. Recite također da objekt ima početno ubrzanje od 10 m/s. Moramo pronaći brzinu na w = 12 sekundi. U ovom slučaju to možemo riješiti na sljedeći način:
-
- a (w) = -30
- p (w) = a (w) dw = -30dw = -30w + C
-
-
Da bismo pronašli C, riješit ćemo p (w) za w = 0. Zapamtite da je početno ubrzanje objekta 10 m/s.
-
- p (0) = 10 = -30 (0) + C
- 10 = C, pa je p (w) = -30w + 10
-
-
Sada možemo unijeti w = 12 sekundi.
-
- p (12) = -30 (12) + 10 = -360 + 10 = -350. Budući da je brzina apsolutna vrijednost ubrzanja, brzina objekta je 350 metara u sekundi.
-
Savjeti
- Vježba čini sjajnu! Pokušajte stvoriti vlastito pitanje zamjenom brojeva u gornjem primjeru.
- Ako tražite brz način za vježbanje računa za bolju brzinu izračuna, upotrijebite online kalkulator derivacija i online integralni kalkulator ovdje.






